U7
Transformational Geometry Investigation
Goal:
To explore translations (slides), reflections (flips), rotations (turns) and
dilations (enlargements/reductions) on a coordinate plane.
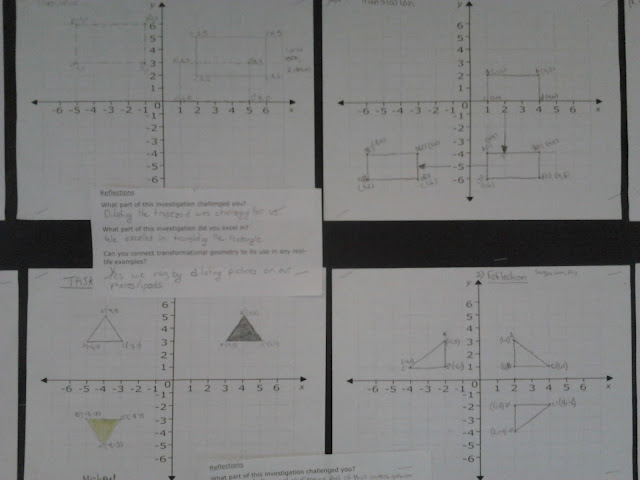
Task 1
· Plot
and label anywhere on the coordinate plane a rectangle of any size; label the coordinates ABCD.
· Translate
(slide) it anywhere 2 different ways.
· Plot
and label the new coordinates of the first translated rectangle as A¹B¹C¹D¹ and
the second translated rectangle as A²B²C²D².
Task 2
·
Plot and label anywhere on the coordinate
plane a triangle (isosceles,
equilateral, right angle or scalene) of any size; label the coordinates ABC.
·
Reflect
(flip) it in the y-axis; plot and label the new coordinates of this reflected
triangle as A¹B¹C¹.
·
Reflect
(flip) the starting triangle in the
x-axis; plot and label the new coordinates of this reflected triangle as
A²B²C².
Task 3
·
Plot and label any irregular shape (i.e. a letter, an arrow) of your choice anywhere
on the coordinate plane; label the coordinates ABCD…
·
Rotate (turn)
it clockwise 90° about any one of its
points (hold down that specific coordinate and turn – use a manipulative);
plot and label the new coordinates of this rotation A¹B¹C¹…
·
Rotate (turn)
the starting irregular shape
counter-clockwise 180°; plot and label the new coordinates of this rotation
A²B²C²…
Task 4
·
Plot and label a trapezoid anywhere on the coordinate plane; label it ABCD.
·
Dilate
(enlarge or reduce) it; plot and label its new coordinates A¹B¹C¹D¹
Reflections
What part of this
investigation challenged you?
What part of this
investigation did you excel in?
Our Reflections:
- Rotations on an anchored point were challenging but easier by creating a manipulative
- Rotations about the origin, spaced equally from the x/y-axis proved to be challenging
- Dialations in a given spot proved challenging when shrinking or enlarging
- Plotting coordinates in an (x,y) formation sometimes proved challenging
- Translations and reflections were very manageable
- We connected transformational geometry to a variety of real-life applications including:
-rotations of pictures on camera or in picture gallery
-fashion textile prints
-architectural design/decor, bridges
-graphic design (logo, emblems)
-class artwork involving rotations and dilations
-class artwork involving rotations and dilations
-car design (headlights/tail lights, wheels)